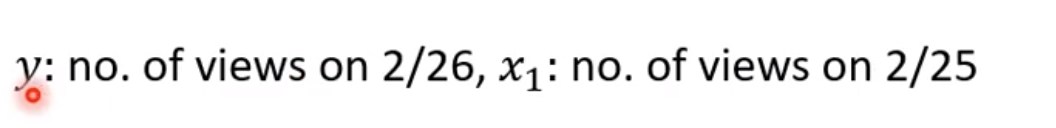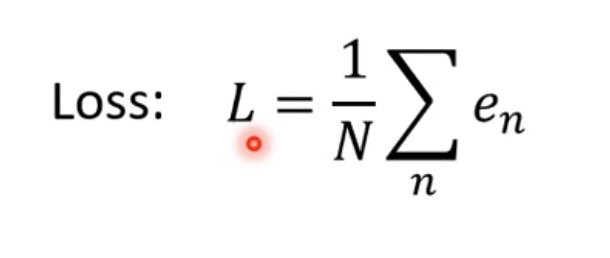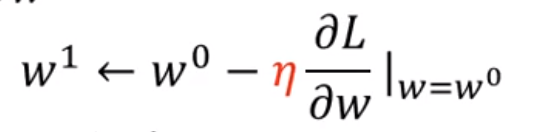1.深度学习机器学习基本概念(上)
1. Machine Learning
什么叫机器学习,实际就是让机器能够拥有查找函数的方式。机器查找问题的方式就是找函数,因为这个问题过于复杂,所以人类无法简单的寻找到,需要通过计算(人工智能?no,人工计算)
this is refer to looking for function.
对于不同任务的机器学习任务是不同的
- speech recognition 输入的是一段音频,输出的是语句,“how are you”
- image Recognition 输入的是一张彩色图像,输出的是对这张图的分类 “猫”
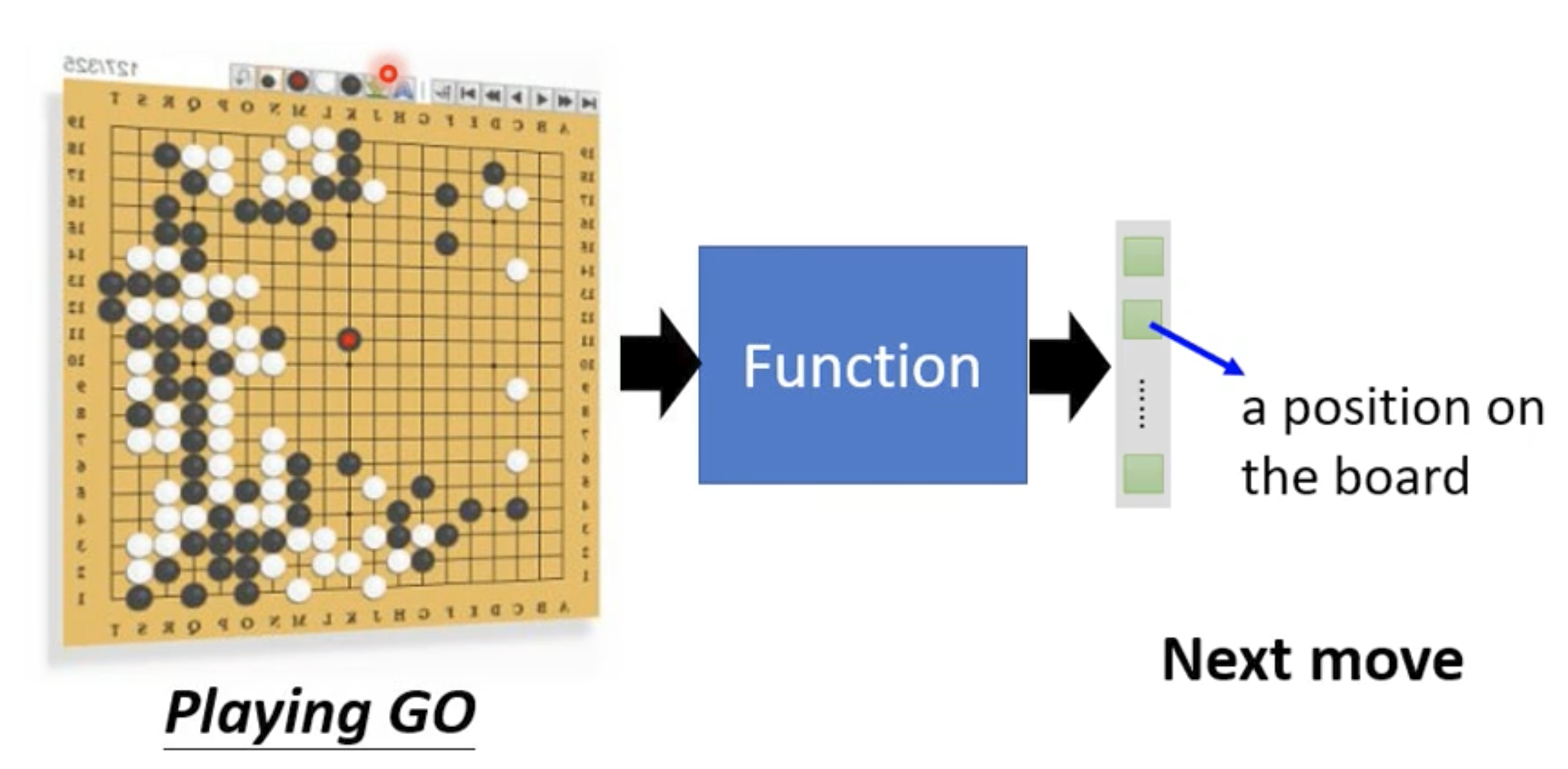
- playing go 输入的是黑子跟白子的位置,输出的是对于下一步的最优解
1.1 Different types of Functions
Rgression: the function outputs a scalar
所谓回归,就是机器的函数输出是个标量
输入:今天2.5PM的值,温度,O3含量,通过这些数据代入到f里,那么就可以预测出名堂PM的值
Classification: given options (classes), the function ouputs correct one.
classfication的目的是进行选择,从一些选项里选择出最可能的选项。
对于垃圾检测机制,选项只有yes/no,是或不是垃圾邮件,这就是最基础的分类应用问题。
对于alpha go其实同样是分类问题,只是alph go的选择比较多,(选择是基于黑棋白棋空余的位置, 19 * 19 -下过的位置)
1.2 structed learning
除了经典的分类和回归问题,还有一个经典的领域问题,就是产生式问题,让机器产生一个有结构的文件,举例来说让机器写一篇文章,让机器画一幅图。也可以说是让机器学会创造。那么机器该如何找一个函式呢?
2. Case Study
通过YouTube channel 来举例
youtuber在意的就是YouTube流量, 因此我们想尝试找到一个函式能够得到youtube预测的流量
因此输入是在2021年2月31日之前每天观看的流量数据,输出是预测第二天或者几天后的观看流量数据
所以这里的任务是做预测。
2.1 找函数的步骤
- 我们要写出一个带有未知函数的参式
$$
y = b + w x_{1}\
$$
w and b 是不确定的参数,是我们猜测的函数
2.2 关于domain knowledg
机器学习其实是需要一些前置知识的,因为你对一个预测问题是需要对这个行业有一些了解,这样可以提出剔除掉一些无关变量,更多的保留和这个问题相关的变量,比如关于房价,我们很直觉的就会认为房子地段,面积是很相关的变量。
2.3 关于Loss
Loss就是损失函数,是关于w,b这两个参数的函数,它衡量了w,b的好坏程度。
2.4 $\hat{y}$和label
我们可以先随机设定w和b,假设w是观看次数为4.8k,也就是1月1日的观看数据,b是1,那么代入可得5.3k,实际的参数可用$\hat{y}$表示,因此y和$\hat{y}$的差距就是error,也就是真实之和预测值的差距。而label就是代表真实值,也就是常规意义说的标签,打标签就是人为的去设定真实值。比如人为的寻找分割图像,人为的分类图像种类。我们只有设定了答案,才能让机器学习。
2.5 Loss,MAE和MSE
每一天相对于前一天都会有一个error,因此可以得到e1,e2,e3,e4….。之后把所有error加起来就得到了loss,除以n(n就是从17年1月1日到12月31日的天数),这步骤也可以叫做加权平均
因为我们关心的误差其实是绝对值,那么可以引申出一个新概念,就叫做平均绝对误差(MAE)

既然可以用绝对值衡量误差,同样也有其他衡量误差的方式,比如平方(MSE)
在回归任务中我们的y和$\hat{y}$都是值,可以用MAE或MSE,但是如果在分类任务中,那得到的是对于每个分类的预测概率值,因此这时候就该用cross-entropy来做
3. Optimization
3.1 寻找w,b
所谓最优化问题,在这个问题里其实就是找到最优解的w,b来获得最小的loss函数。而这个最小的w,b可以用$w_{*}$表示, 优化的方法之一就是梯度下降
3.2 gradient descnet
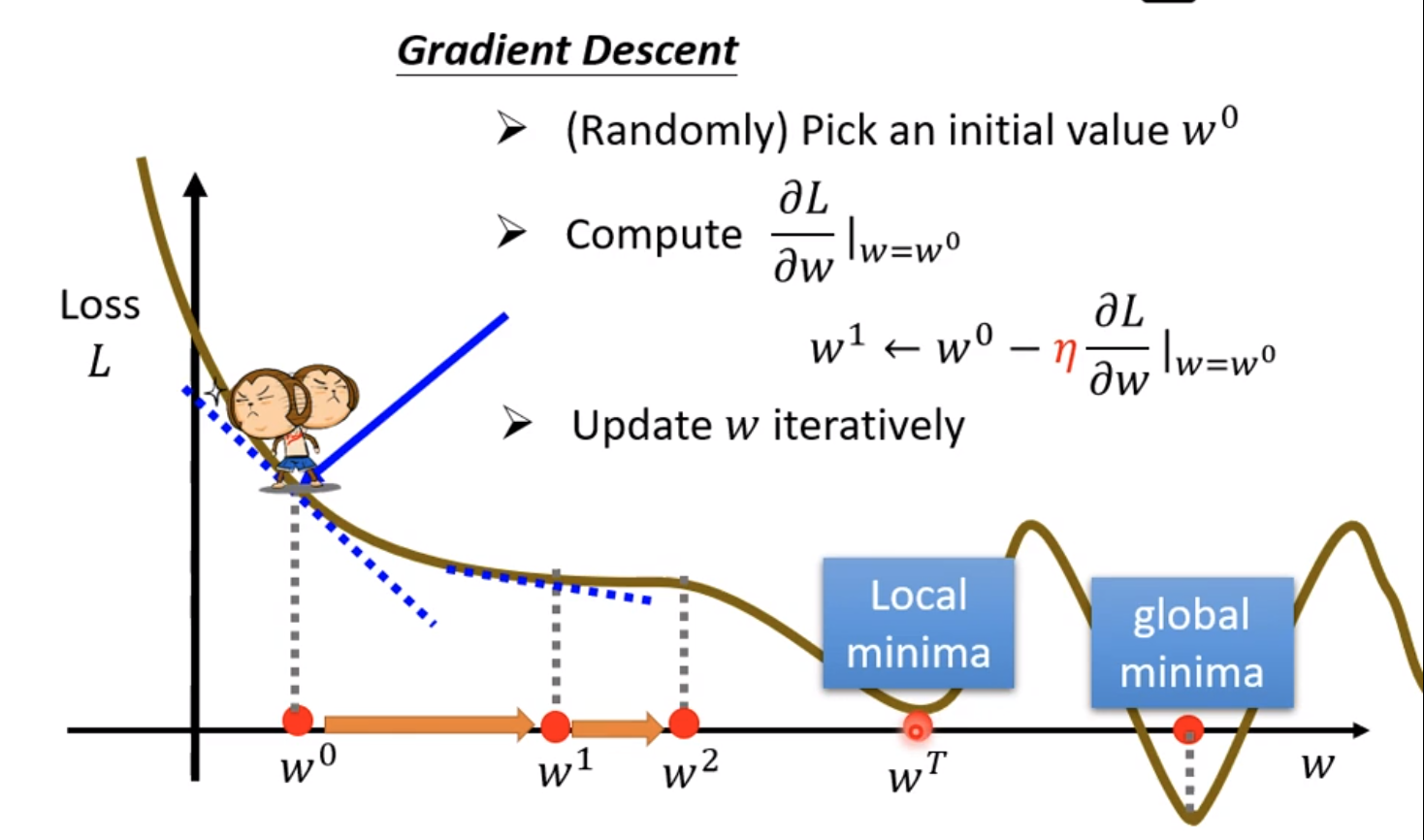
上图画出了梯度下降中找w的变化对于l的影响的图,我们知道斜率就是代表w的变化程度,如果斜率为负,那就说明左边比右边高,因此需要增加w来让loss下降。反之斜率为负,则需要减少让loss上升。因为微积分的知识告诉我们,在f’(x)=0的时候有极值,而这个时候就是斜率为0的时候,也就是最顶峰的时候。
3.3 learning rate
我们找w的过程中要减少或者增加每步的步数变化叫做学习率,这个是自己设定的参数
那么从${w}^{0}$到${w}^{1}$的公式可以写成:
3.4 global minimum和local minimum
如果我们训练的过程中遇到了local minimum就停止了,但是实际上是有global minumum,也就是绝对误差的。但是实际上local minimum是个假问题,原因是?
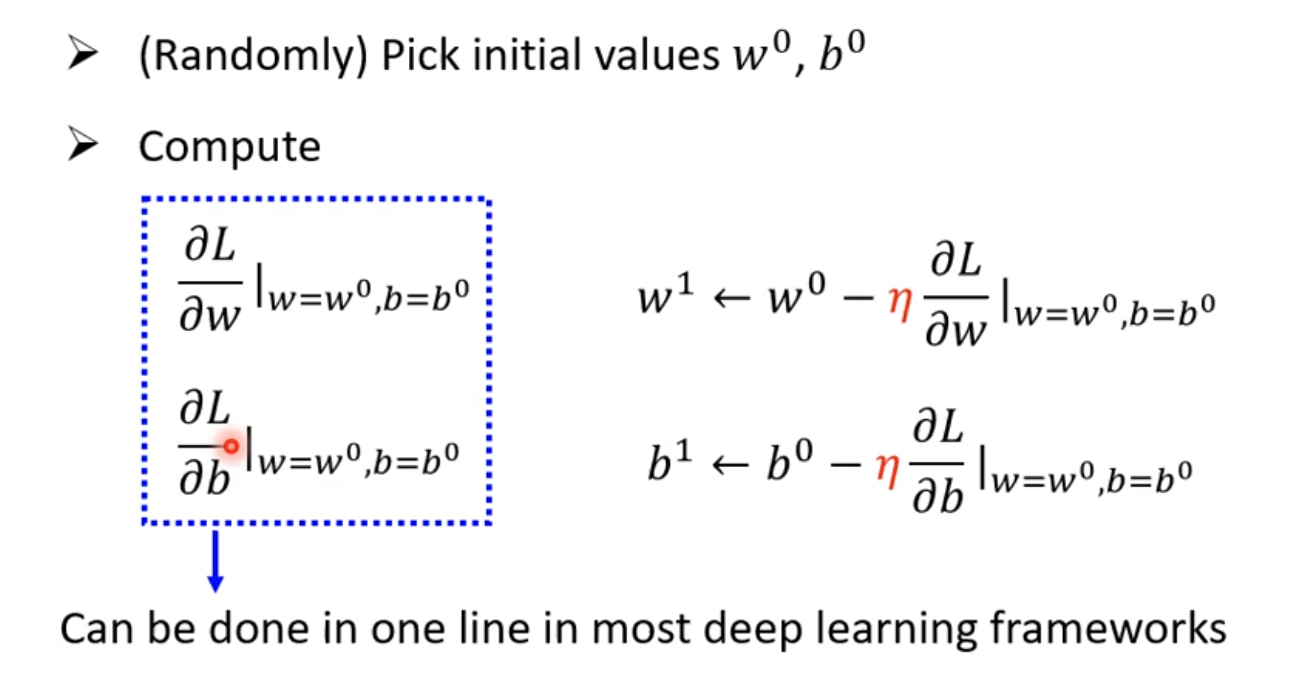
3.5 w,b共同作用下的loss
我们之前算的是只有w变化下的loss变化图,但是公式其实是一样的,那么就可以写成:
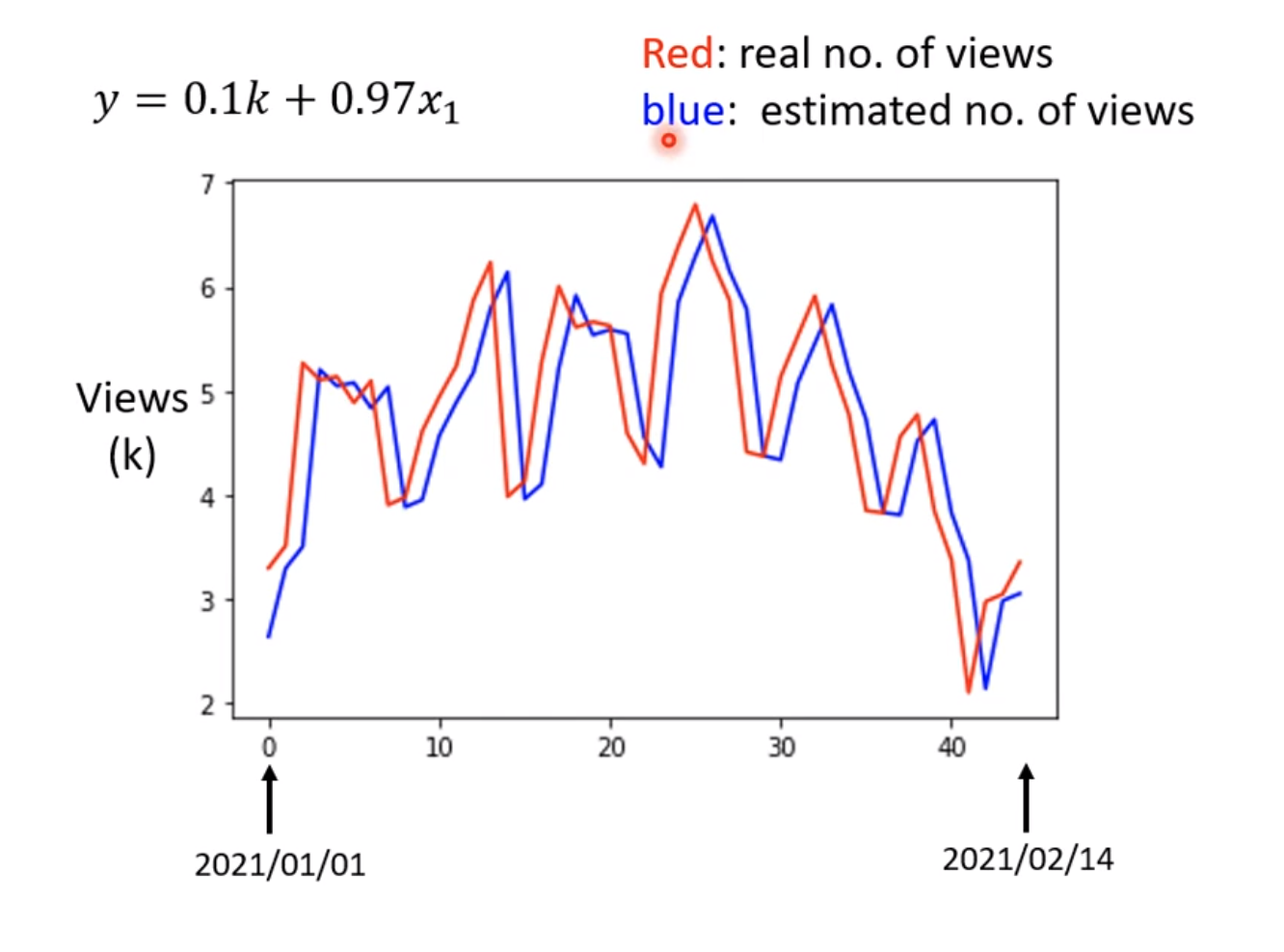
3.6 预测结果图
红色值是真实观看人数数据,蓝色是预测这段期间的观看人数数据。仔细观看图会发现蓝色的图其实就是对于红色图每一个数据点推移了后一天而已。
但是我们仍然从这个图可以看到一些规律,比如每隔七天就会出现下降,这个下降的日期一般是周五到周一。因此我们可以设想新模型不再是每天的预测,而是以七天为周期的模型预测。
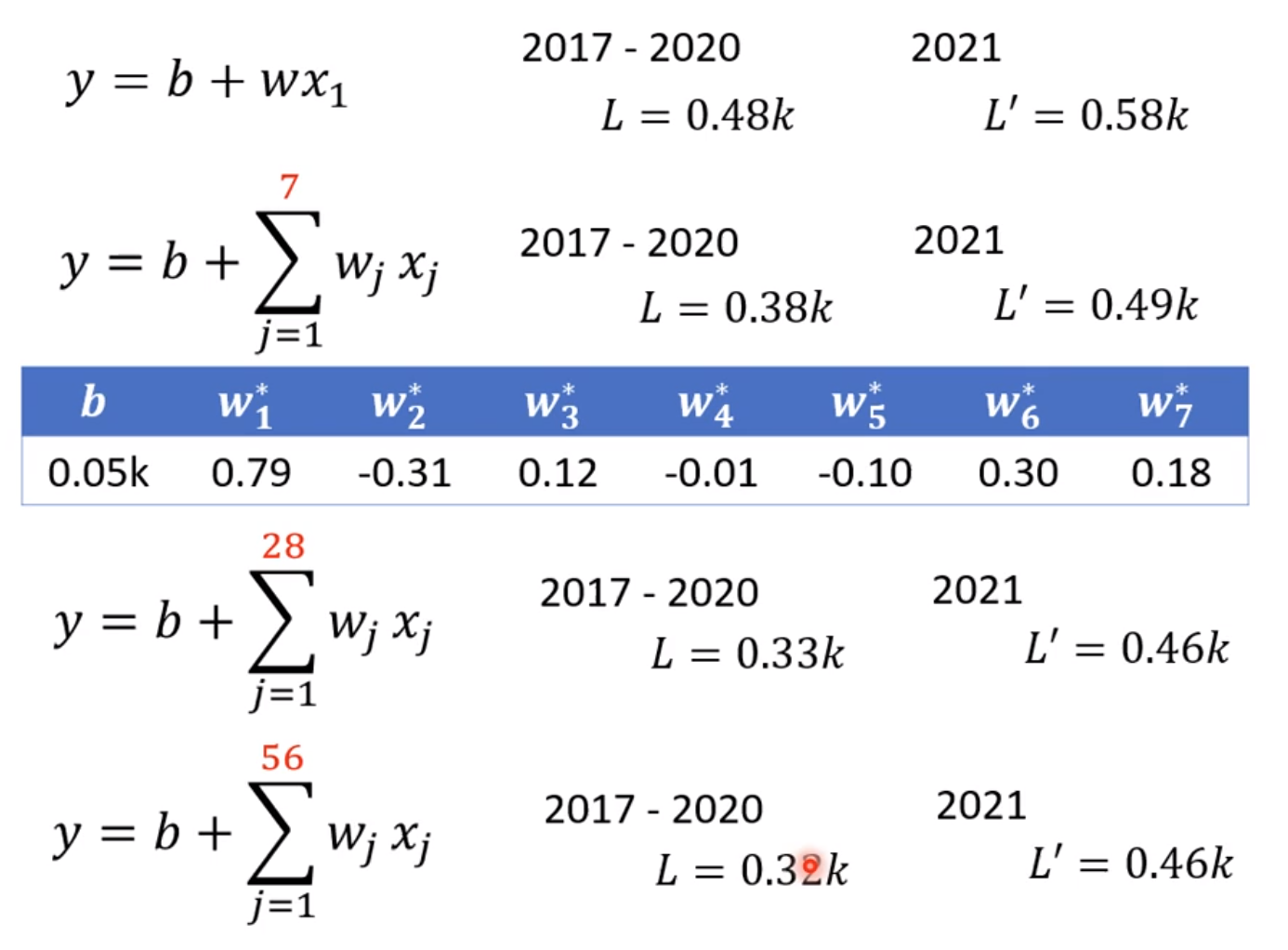
既然可以用七天为周期,是不是也可以用28天,56天为周期进行预测,并且记录每次周期变化的L和L’
可以发现L在逐渐变小,L’也在逐渐变小。
x就是feature,w是weight,加上bias这类模型都可以被称为回归模型,linear models